Results:

This project received a grade of 18, delivering an optimized genetic algorithm by coupling it with Particle Swarm Optimization.

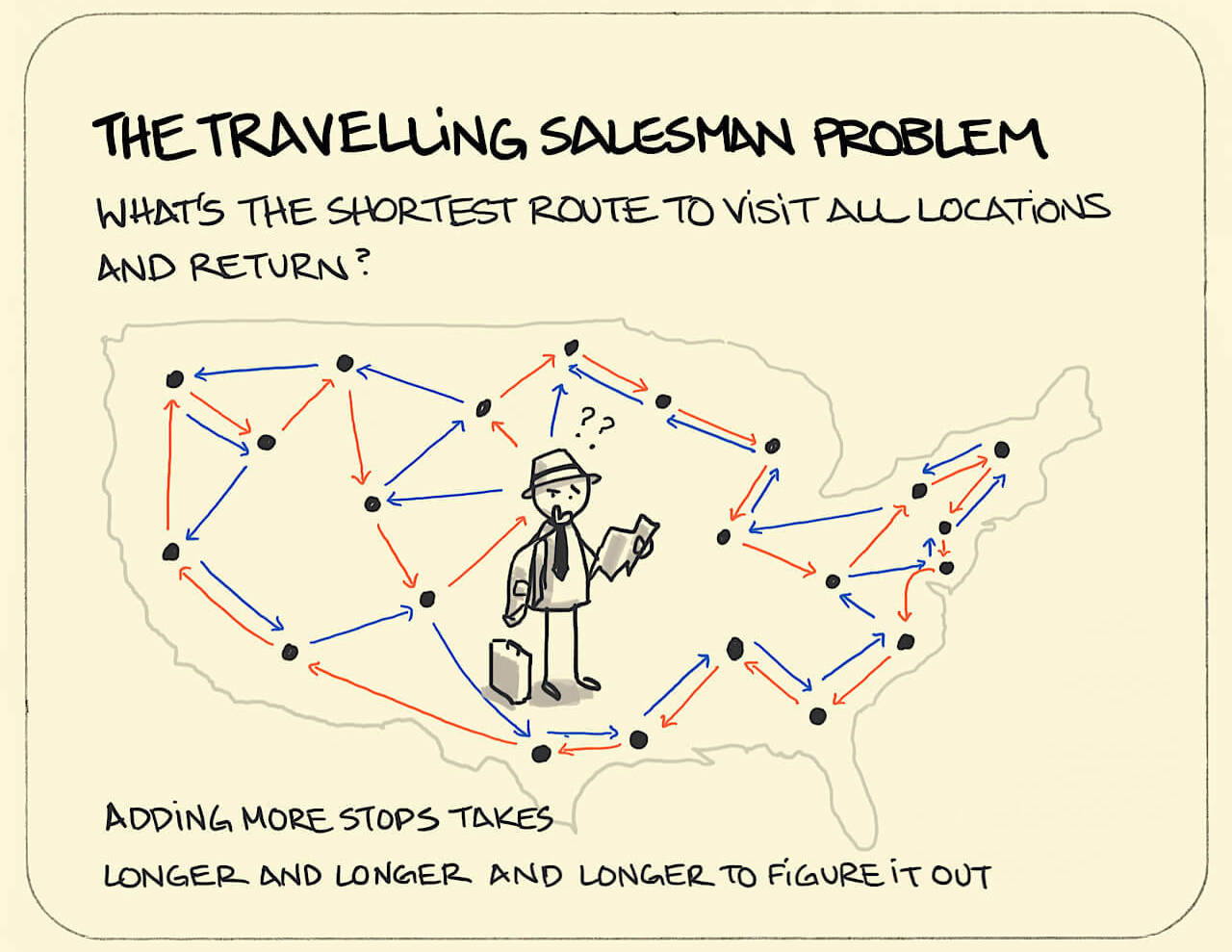
Travelling Salesman With Genetic Algorithm

I focus on solving the Traveling Salesman Problem (TSP), where each route between cities is associated with a specific cost. My goal is to optimize this problem by applying the metaheuristic genetic algorithm to find the most efficient solution.

The Genetic algorithm is an optimization method inspired by natural evolution principles such as selection, crossover, and mutation. It works by creating a population of candidate solutions (called “individuals”) to a given problem. These individuals evolve over generations to improve their quality.

• Initialization: An initial population of solutions is generated randomly.
• Evaluation: Each individual is evaluated using a fitness function that measures solution quality.
• Selection: The best individuals are selected to reproduce.
• Crossover: Selected individuals exchange segments of their solutions to produce a new generation.
• Mutation: Some solutions undergo random modifications to maintain genetic diversity.
• Repetition: The process repeats over multiple generations until an optimal or satisfactory solution is found.

The genetic algorithm is effective for complex problems because it explores a large solution space and can avoid local minima.

Improvements to the Genetic Algorithm

A possible enhancement of the genetic algorithm involves integrating adaptation and diversification mechanisms to improve convergence and avoid getting trapped in suboptimal solutions. Here are some specific strategies:

• Adaptive Mutation: Instead of using a fixed mutation rate, dynamically adjust the rate based on population diversity. For example, if diversity decreases and solutions converge too quickly to the same point, increase the mutation rate to explore new regions of the solution space.
• Intelligent Crossover: Rather than random crossover, use a guided crossover based on solution similarity. This allows combining the most promising parts of parent solutions. For example, in TSP, a crossover could try to preserve optimal subtours from the parents.
• Solution Repair: Sometimes mutations or crossovers produce invalid solutions (e.g., in TSP, routes that visit the same city twice). Repair mechanisms can correct these while maintaining solution validity.
• Hybridization with Local Search Algorithms: Combining the genetic algorithm with a local optimization method (such as tabu search or descent algorithms) refines found solutions. After generating new solutions through crossover, a local search phase can further improve individuals.
• Multiple Populations and Migration: Divide the population into isolated subpopulations (“islands”) that evolve independently for several generations, then allow migration between them. This maintains greater diversity in the overall population and prevents premature convergence.

These improvements make the genetic algorithm more robust and efficient, especially when applied to complex problems like the Traveling Salesman Problem.